Für die Kinematik dieses parallelen Mechanismus' braucht man eine 'Closing Equation', mit der man die geschlossene kinematische Kette berechnen kann. Der Ansatz ist Folgender:
1. Die Kippungen der Plattform in x- und y-Richtung kann durch Drehmatrizen Rx(phi) und Ry(theta) beschrieben werden.
Die Ansatzpunkte für die distalen Arme in Plattform-Ebene werden durch die Drehmatrix Rx * Ry im Raum gekippt.
Code: Alles auswählen
p_m = [ -v*cos(theta), - v * sin(phi)* sin(theta) - w * cos(phi), +v * cos(phi)*sin(theta) - w * sin(phi)+ hs]
p_p = [ +v*cos(theta), + v * sin(phi)* sin(theta) - w * cos(phi), -v * cos(phi)*sin(theta) - w * sin(phi)+ hs]
2. Die Aktuatoren drehen die proximalen Arme um die y-Achse. Die Endpunkte dieser Arme sind ebenfalls Ansatzpunkte für die distalen Arme (Das sind die mit den Kugelgelenken)
Code: Alles auswählen
q_m = [ u * cos(alpha) - r, -w, -u * sin(alpha) + h ]
q_p = [ u * cos(beta) + r, -w, -u * sin(beta) + h ]
3. Die Differenzen der Ansatzpunkte (1-2, jeweils links und rechts) müssen dann immer die gleiche Länge (hier l) haben.
Code: Alles auswählen
eq_m = (p_m[0] - q_m[0])**2 +(p_m[1] - q_m[1])**2 + (p_m[2]-q_m[2])**2 - l**2
eq_p = (p_p[0] - q_p[0])**2 +(p_p[1] - q_p[1])**2 + (p_p[2]-q_p[2])**2 - l**2
Beide Bedingungen müssen simultan und unabhängig voneinander erfüllt sein, was mit folgender "Clsoing Equation" erreicht werden kann:
(Die Quadrierungen verhindern, dass der linke den rechten Term kompensiert)
Für mein Modell gelten folgende Parameter:
Code: Alles auswählen
u = 7 # proximal arm length
v = 12 # x/2 Tilt Platform
w = 8 # y/2 Tilt Platform
r = 19 # x-pos Actuator
h = 8 # z-pos Actuator
hs = 7 # central ball joint Tilt Platform ( instead of cardanic frame for simplicity)
l = 5 # distal arm length
Die Lösung der Closing-Equation kann man mit der nlspol-Funktion von Casadi
https://web.casadi.org/docs/ machen, eine python-Bibliothek, die algorithmische Differentiation beherrscht. D.h. es werden Variablen phi, theta, alpha und beta definiert. Die Funktionen bleiben erhalten und können "algorithmisch" differenziert werden, was für die Numerik von Vorteil ist. Hier werden die Stellwinkel für die Horizontalposition der Plattform berechnet:
Code: Alles auswählen
# first: caclulate Zero-Position:
nlp = {'x': actangle, 'f': cleq, 'p': tiltangle}
nlp_solver = casadi.nlpsol('backward', 'ipopt', nlp, opts)
x0old = [0.1,0.1]
solution = nlp_solver(x0=x0old, p=[0,0])
r= np.array( solution['x'] )
print( degrees(r[0]), degrees(r[1]))
Das Bild zeigt eine Schaar von Lösungen für phi und theta der Plattform-Kippung in Abhängigkeit des "gleichsinnigen Stellwinkels" (D.h. beide Aktuatoren werden gleichsinnig geändert). Die grünen Kurven geben die Kippung um y (links/rechts) an. Die blauen Kurven entsprechen diskreten "gegensinnigen Stellwinkel-Einstellungen". (Kippung um x (vorne/hinten)
Man sieht, dass der Verlauf der Kippung kaum vom gleichsinnigen Stellwinkel abhängt und dass die Kippung mit dem "gleichsinnigen Stellwinkel" fast linear ist.
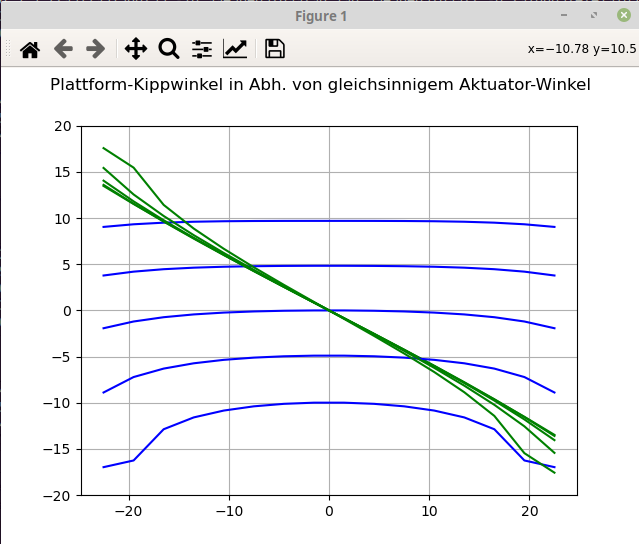
- Bildschirmfoto vom 2023-05-24 23-04-17.png (63.1 KiB) 298 mal betrachtet
Gleiches gilt für die "andere Richtung"
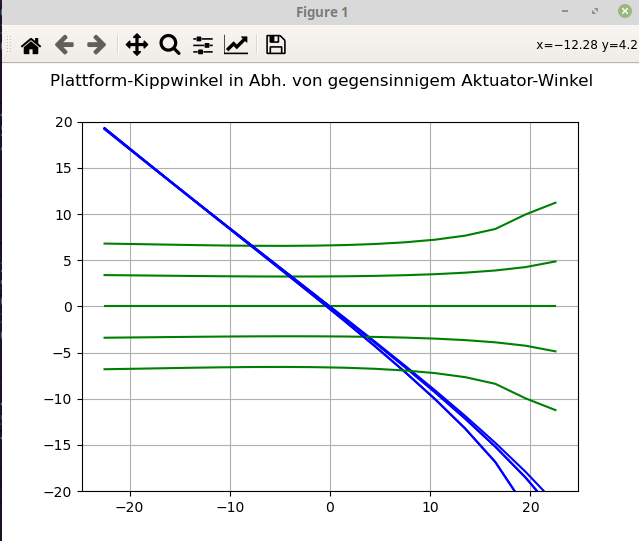
- Bildschirmfoto vom 2023-05-24 23-06-21.png (53.48 KiB) 298 mal betrachtet
D.h. die Kippungen sollten durch lineare Funktionen der stellwinkel angenähert werden können. Bei 10 Grad Tilt nach vorne kommt es zum "Übersprechen" der Richtungen. Aber für kleine Winkel passt das.
Ich hoffe, dass ich das richtig berechnet habe. Weshalb die untere Kurven nicht symmetrisch sind, kann ich nicht sagen. Das sollte nicht so sein. Vielleicht ist ja doch noch ein Denkfehler drin.
) Die Drehscheiben für die Arme werden über einen Power-Motor mit Schnecke über Z30 bewegt. Der Power-Motor könnte über Z10 locker ein Z40 antreiben. Damit bekomme ich die Zitterbewegungen allerdings gar nicht weg, wie ich mich auch anstelle. Ich frage mich, ob PID-Regler für die Positionierung der optimale Ansatz ist. Wie macht Ihr das bei Euren Modellen?
